Reactions

Modules

Visualization

Reactions are visualized with the open-source library cytoscape.js (example of interactive version; more can be found under Experiments.)

Data Structure

The classes ChemData and Reaction store the data about all applicable reactions, including stoichiometry, reaction rates, reaction orders, thermodynamic data, and macromolecule data. They also provide methods to set and view those values. Details in the Guide.

At a later date, graph databases (the foundation of our sister open-source project BrainAnnex.org) will be utilized. For now, a simpler in-memory data structure is being used.
As of version Beta 26.3, installing Life123 automatically includes the NeoAccess library for connecting to Neo4j graph databases (details.) It will start being fully utilized in later versions.

Computations

Single-compartment reactions are handled with the methods of the classes UniformCompartment, ReactionDynamics and VariableTimeSteps. Details in the Guide.

Classes dealing with the spatial element, namely BioSim1D, BioSim2D and BioSim3D, create ad-hoc compartments for the reactions – typically (but not necessarily) their bins.

General Background and Terminology

Recommeded reading: Reaction Kinetics, by Claire Vallance

Consider a generic chemical reaction such as:

\(\require{\mhchem} \ce{aA +bB <=>[k_F][k_R] cC + dD}\)

where A, B, C, D are chemical species, while a, b, c, d are integers (the stoichiometry coefficients.) k_F and k_R are, respectively, the forward and reverse rate constants, as detailed below.

A and B are generally referred as the reactants, while C and D are the products of the reaction. However, to be noted that the reaction goes in both directions at the same time – imagine two adjacent rooms, where some people go from one to the other, while others go in the opposite direction.

As customary, we'll use square brackets, as in \([A]\) , etc, to indicate the concentrations. Generally, those are functions of time, \([A](t)\) , but we'll often omit the \((t)\)

If the concentrations change with time, the reactants as well as the reaction products must change in lockstep to satisfy the stoichiometry (i.e. maintain the relative balances.)

EXAMPLE

The initial system contains the following numbers of molecules:
A: 100 , B: 300 , C: 50 , D: 200
and the reaction is 2 A + 4 B <-> 3 C + 2 D (i.e. with coefficients a = 2, b = 4, c = 3, d = 2)

Lets say that 2 molecules of A react with 4 molecules of B, and as a result they transform into 3 molecules of C and 2 of D.
The net effect will be:
ΔA = -2 ; ΔB = -4 ; ΔC = 3 ; ΔD = 2

This corresponds to "1 unit of reaction". A larger reaction could be double, triple, etc, the amounts – but they all need to change in lockstep:

\(- \Delta A/a = - \Delta B/b = \Delta C/c = \Delta D/d\)

The flip in the signs indicates that some chemicals are produced while others are consumed. In the forward reaction, A and B are consumed, while C and D are produced; in the reverse reaction, it's the other way 'round.

The ratio \(\Delta C/c\) (the concentration of a product that is formed in a unit of time, adjusted for its stoichiometry coefficient) is called reaction rate, also known as reaction velocity.

Switching from Discrete to Continuous

Upon shifting our attention to large numbers of molecules in a liquid solution, one typically starts using real number and concentrations; for example, at time t₀, [A](t₀) = 12.425 billion molecules per liter.

Using primes to indicate the time derivatives (i.e. instantaneous rate of change) of the Concentrations functions, and omitting the (t) parts, the above example generalizes to:

\(- \ {1 \over a} [A]' = - \ {1 \over b} [B]' = \ {1 \over c} [C]' = \ {1 \over d} [D]' \)

The expressions with the [A] and [B] concentrations indicate the rate of change of the reactants; the expressions with the [C] and [D] concentrations indicate the rate of change of the reaction products.

Again, \( \ {1 \over c} [C]' \) is defined as the reaction rate.

Numerical Methods

Don't worry – Life123 hides the details "under the hood"! This section is for those interested in the numerical methods...

To solve the ordinary differential equations for the chemical reactions, the simple and intuitive forward Euler method is being used at present. Grids of variable spacing (for variable time resolution) are also implemented with various heuristics.

At a later date, this "in house" approach will be complemented by the use of open-source libraries for solving ode's by various methods.

Solving the Reaction Equations

From the Kinetic Theory of chemical reactions, the forward rate is proportional to \([A]^{O_A} * [B]^{O_B} \) , and the proportionality factor is called forward rate constant.

The exponents O_A and O_B are, respectively, the orders of the reaction relative to A and B. The orders have to do with the detailed mechanism of the reaction – in particular, whether the reactions are elementary or composite – and they are measured experimentally, or estimated by means of Molecular Dynamics computations.
IMPORTANT: the orders of the reaction are NOT necessarily the same as the stoichiometry coefficients!

\(\require{\mhchem} \ce{aA +bB <=>[k_F][k_R] cC + dD}\)

Intuitively, the higher the concentrations of A and B are, then the higher the odds that they will collide and move the reaction forward.

\(Forward \ Rate = k_F * [A]^{O_A} * [B]^{O_B}\)

similarly:

\(Reverse \ Rate = k_R * [C]^{O_C} * [D]^{O_D}\)

Intuitively, the higher the concentrations of C and D are, then the higher the odds that they will collide and move the reaction in the reverse direction.

Note the somewhat unfortunate nomenclature: the forward or reverse rates should not be confused with the rate constants (k_F and k_R )

Note that the difference (Forward Rate - Reverse Rate) is the measure the imbalance towards the forward direction of the reaction (i.e., the tendency of the reaction to proceed forward, per unit of time.) That's the Reaction Rate that we defined before. I.e.:

\(Reaction\ Rate = Forward\ Rate - Reverse\ Rate\).

Substituting from above:

\(Reaction\ Rate = \color{purple}{ \left( k_F * [A]^{O_A} * [B]^{O_B} \right) - \left( k_R * [C]^{O_C} * [D]^{O_D} \right) } \)

For the reaction products, as mentioned in the previous section:

\({1 \over c} [C]' = {1 \over d} [D]' = Reaction\ Rate \)

and, similarly for the reactants:

\({1 \over a} [A]' = {1 \over b} [B]' = -\ Reaction\ Rate \)

For the reactants, for example for A, and changing the notation to \({d \over dt }[A](t)\) to emphasize the ordinary differential equation (ode):

\({d \over dt }[A](t) = -a * \ Reaction\ Rate = -a * \color{purple}{ \left\{ k_F * [A](t)^{O_A} * [B](t)^{O_B} -k_R * [C](t)^{O_C} * [D](t)^{O_D} \right\} } \)

For the reaction products, for example for C, the sign is reversed:

\({d \over dt }[C](t) = c * \ Reaction\ Rate = c * \color{purple}{ \left\{ k_F * [A](t)^{O_A} * [B](t)^{O_B} -k_R * [C](t)^{O_C} * [D](t)^{O_D} \right\} } \)

To better see the above equation as a typical ode, it might help to write [A](t) as f(t), and to change the notation of the concentration functions to \(C_X(t)\), where X is the chemical species. Then the equation for A's concentration becomes:

\(\color{brown}{f'(t)} = -a * \left\{k_F * \color{brown}{f(t)}^{O_A} * C_B(t)^{O_B} - k_R * C_C(t)^{O_C} * C_D(t)^{O_D} \right\}\) , where f(t) is the concentration of A.

If the change of notation doesn't make it easier for you, please disregard! We won't be using it further.

The initial conditions are the given concentrations at time t=0 : \([A](0) , [B](0)\) , etc. We'll refer to those values as A₀, B₀, etc

One straightforward way to solve the above ode is to use the forward Euler method to start with the values at t=0, namely A₀, B₀, C₀, D₀, and then compute all the values at a later time step :

If we introduce subscripts to indicate values at discrete times, and define:

\(\text{delta_forward}(n) = \left( k_F * [A]_n^{O_A} * [B]_n^{O_B} - k_R * [C]_n^{O_C} * [D]_n^{O_D} \right)\)

then, for the reactants:

\([A]_{n+1} = [A]_n - (\Delta t) * a * \text{delta_forward}(n)\)

\([B]_{n+1} = [B]_n - (\Delta t) * b * \text{delta_forward}(n)\)

and for the reaction products the sign flips:

\([C]_{n+1} = [C]_n + (\Delta t) * c * \text{delta_forward}(n)\)

\([D]_{n+1} = [D]_n + (\Delta t) * d * \text{delta_forward}(n)\)

where \(\Delta t\) is the desired step size, and n = 0, 1, 2, ....

How Many Equations Do We Have?

At the end of last section, it might appear that we're lugging around 4 equations but, in fact, if we compute the change of concentrations of any species, then the other ones are simply determined by the stoichiometry.

For example, let's say we know \(\color{blue}{[A](t)}\) at some time t , as well as all the initial concentrations A₀, B₀, C₀, D₀.

Then:
\([B](t) = B_0 + \Delta B = B_0 + b { \Delta B \over b} = B_0 + b { \Delta A \over a} = B_0 + { b \over a} (\color{blue}{[A](t)} - A_0) = { b \over a} \color{blue}{[A](t)} + (B_0 - {b \over a} A_0)\)

So, [B](t) is just a linear function of [A](t)

For [C](t) and [D](t) there's a sign flip, going from reactant to product of reaction:

\([C](t) = C_0 + \Delta C = C_0 + c { \Delta C \over c} = C_0 \color{red}- c { \Delta A \over a} = C_0 - { c \over a} (\color{blue}{[A](t)} - A_0) = -{ c \over a} \color{blue}{[A](t)} + (C_0 + {c \over a} A_0)\)

\([D](t) = D_0 + \Delta D = D_0 + d { \Delta D \over d} = D_0 \color{red}- d { \Delta A \over a} = D_0 - { d \over a} (\color{blue}{[A](t)} - A_0) = -{ d \over a} \color{blue}{[A](t)} + (D_0 + {d \over a} A_0)\)

EXAMPLE

Let's revisit the earlier example with A₀ = 100 , B₀ = 300 , C₀ = 50 , D₀ = 200
and the reaction 2 A + 4 B <-> 3 C + 2 D   (with coefficients a = 2, b = 4, c = 3, d = 2)

Imagine that at some time t*, our ode solver tells us that [A](t*) = 80.    What can we infer about the other concentrations?
Using the above formulas:

\([B](t^*) = { b \over a} \color{blue}{[A](t^*)} + (B_0 - {b \over a} A_0) = { 4 \over 2} \color{blue}{80} + (300 - {4 \over 2} 100) = 260\)

\([C](t^*) = - { c \over a} \color{blue}{[A](t^*)} + (C_0 + {c \over a} A_0) = - { 3 \over 2} \color{blue}{80} + (50 + {3 \over 2} 100) = 80\)

\([D](t^*) = - { d \over a} \color{blue}{[A](t^*)} + (D_0 + {d \over a} A_0) = - { 2 \over 2} \color{blue}{80} + (200 + {2 \over 2} 100) = 220\)

Those values make eminent sense once you realize that we had "10 units of reaction" for 2 A + 4 B <-> 3 C + 2 D, which consumed 20 of A and 40 of B, while producing 30 of C and 20 of D.

Note that A₀ + B₀ + C₀ + D₀ = 650 , while A(t*) + B(t*) + C(t*) + D(t*) = 640.   That makes sense, too, because the reaction starts with 6 molecules and ends up with 5 (after their atomic constituents get reshuffled); that's a loss of 1 molecule per "unit of reaction" - hence a loss of 10 in our case.

EXAMPLE – How does the sum of all the chemical concentrations change from time 0 to t?

If we use C_X(t) to indicate the concentration of chemical X at time t, and take the sums over ALL chemicals (reactants and products):

\(\begin{align} \left[ \displaystyle\sum_{X} C_X(t) \right] - \left[ \displaystyle\sum_{X} C_X(0) \right] = [A(t) + B(t) + C(t) + D(t)] - [A_0 + B_0 + C_0 + D_0] \\ = A(t) + (B_0 + b { \Delta A \over a}) + (C_0 - c { \Delta A \over a}) + (D_0 - d { \Delta A \over a}) - A_0 - B_0 - C_0 - D_0 \\ = A(t) - A_0 + b { \Delta A \over a} - c { \Delta A \over a} - d { \Delta A \over a} \\ = a { \Delta A \over a} + b { \Delta A \over a} - c { \Delta A \over a} - d { \Delta A \over a} \\ = { \Delta A \over a }[ (a + b) - (c + d)] \end{align}\)

The above equality could be used as form of validation for a single-equation solver.

Using date from the previous example:
\({ \Delta A \over a }[ (a + b) - (c + d)] = {(80-100) \over 2} [(2+4) - (3+2)] = -10 * 1 = -10 \) , just as we had noted above.

Exact Solution of the 1st Order Reaction A <=> B

An exact analytical solution is available in some scenarios; for example the simple reaction:

\(\require{\mhchem} \ce{A <=>[k_F][k_R] B}\)

We'll write the concentrations of the reactant A and the product B, as a function of time, as A(t) and B(t).

From the stochiometry, we can see that for every molecule consumed of A, one molecule of B is produced ‐ and vice versa. Therefore : A(t) + B(t) = TOT , for some constant TOT. That's equation 1, below.

If the reaction is elementary (occurring in a single step), or can modeled as such, the net rate of production of B is its production rate (which is proportional to the concentration of A and to the forward rate constant k_F) , minus its consumption rate (i.e reverse reaction, which is proportional to the concentration of B and to the reverse rate constant k_R). That goes into equation 2.

Finally, we need to specify some initial condition; for example that at time 0, the concentration of A is some value A₀ . That gives us equation 3.

\(\begin{cases} & A(t) + B(t) = TOT && (1) \\ \\ & B\ '(t) = k_F \ A(t) - k_R \ B(t) && (2) \\ \\ & A(0) = A_0 && (3) \\ \end{cases}\)

Note that there's no need to specify an equation for the rate of change A'(t) , because it follows from (2) and (1) :

\( A\ '(t) = {d\over dt} A(t) = {d\over dt} [TOT- B(t)] = - B\ '(t) = k_R \ B(t) - k_F \ A(t) \)

As expected, A is produced from B based on the reverse rate constant k_R, and is consumed based on the forward rate constant k_F

Also note that at time t=0 :

\(A(0) + B(0) = TOT \quad , i.e. \quad A_0 + B_0 = TOT\) , where we're definining B₀ = B(0)

The system of equations (1) thru (3) has the following exact, analytical solutions for A(t) and B(t) :

\(A(t) = [A_0 - {k_R \over k_F+k_R}TOT]\ \color{blue}{e^{-(k_F+k_R)t}} + {kR \over k_F+k_R} TOT\)

\(B(t) = [{k_R \over k_F+k_R}TOT - A_0 ]\ \color{blue}{e^{-(k_F+k_R)t}} + {kF \over k_F+k_R} TOT\)

we're emphasizing in blue the identical exponential part. Everything else is just constants.

Notice that at equilibrium, as t -> ∞ , the exponentials go to zero, and A(t) approaches kR * TOT /(kF + kR) , while B(t) approaches kF * TOT /(kF + kR). The ratio B(t)/A(t) at equilibrium is kF /kR , which is the reaction's equilibrium constant, as expected.

The above equations may be explored in Mathematica with:

A[t_] = (A0 - (kR TOT) / (kF + kR)) Exp[-(kF + kR) t] + kR TOT / (kF + kR)
B[t_] = ((kR TOT) / (kF + kR) - A0) Exp[-(kF + kR) t] + kF TOT / (kF + kR)

Simplify[A[t] + B[t]]
produces: TOT (satisfying equation 1)

Simplify[D[B[t], t] - kF * A[t] + kR * B[t]]
produces: 0 (satisfying equation 2)

A[0]
produces: A0 (satisfying equation 3)

Note that the system of equations (1) thru (3) may be solved symbolically in Mathematica with:

DSolve[{A[t] + B[t] == TOT, D[B[t], t] == kF A[t] - kR B[t], A[0] == A0}, {A[t], B[t]}, t]

(with some algebraic rearranging, the answers given by Mathematica can be shown to be equivalent to the more concise form we gave above.)

Numerical Instability

Numerical instability is a bane of solving ODE's! One advantage of dealing with variables that represent chemical concentrations, is that they must be always be non-negative. This constraint can be utilized to help detect instability: chemical concentrations assuming negative values may be used as an instability warning - not enough to catch all instances of instability, but helpful nonetheless.

3 scenarios may be distinguished. Illustrative examples are shown; "Delta_1" and "Delta_2" are the changes to the concentration of a particular chemical, arising, respectively, from two separate reactions.

	Description	Initial conc. (of some chemical)	Delta_1 (caused by reaction 1)	Delta_2 (caused by reaction 2)	Final conc.	Notes
scenario 1	A reaction causes a dip (of any chemical concentration) into the negative, and the combined other reactions fail to remedy it	20	-30	+5	-5
scenario 2	A reaction causes a dip into the negative, and the combined other reactions counterbalance it enough to remedy it (return to positive)	20	-30	+30	20	though "counterbalanced", this is still regarded as a sign of numerical instability
scenario 3	Scenario 3 : No single reaction causes any negative concentration, but - combined - they do	20	-15	-15	-10

Description

Initial conc.

(of some chemical)

Delta_1 (caused by reaction 1)

Delta_2 (caused by reaction 2)

Final conc.

Notes

scenario 1

A reaction causes a dip (of any chemical concentration) into the negative, and the combined other reactions fail to remedy it

-30

-5

scenario 2

A reaction causes a dip into the negative, and the combined other reactions counterbalance it enough to remedy it (return to positive)

-30

+30

though "counterbalanced", this is still regarded as a sign of numerical instability

scenario 3

Scenario 3 : No single reaction causes any negative concentration, but - combined - they do

-15

-10

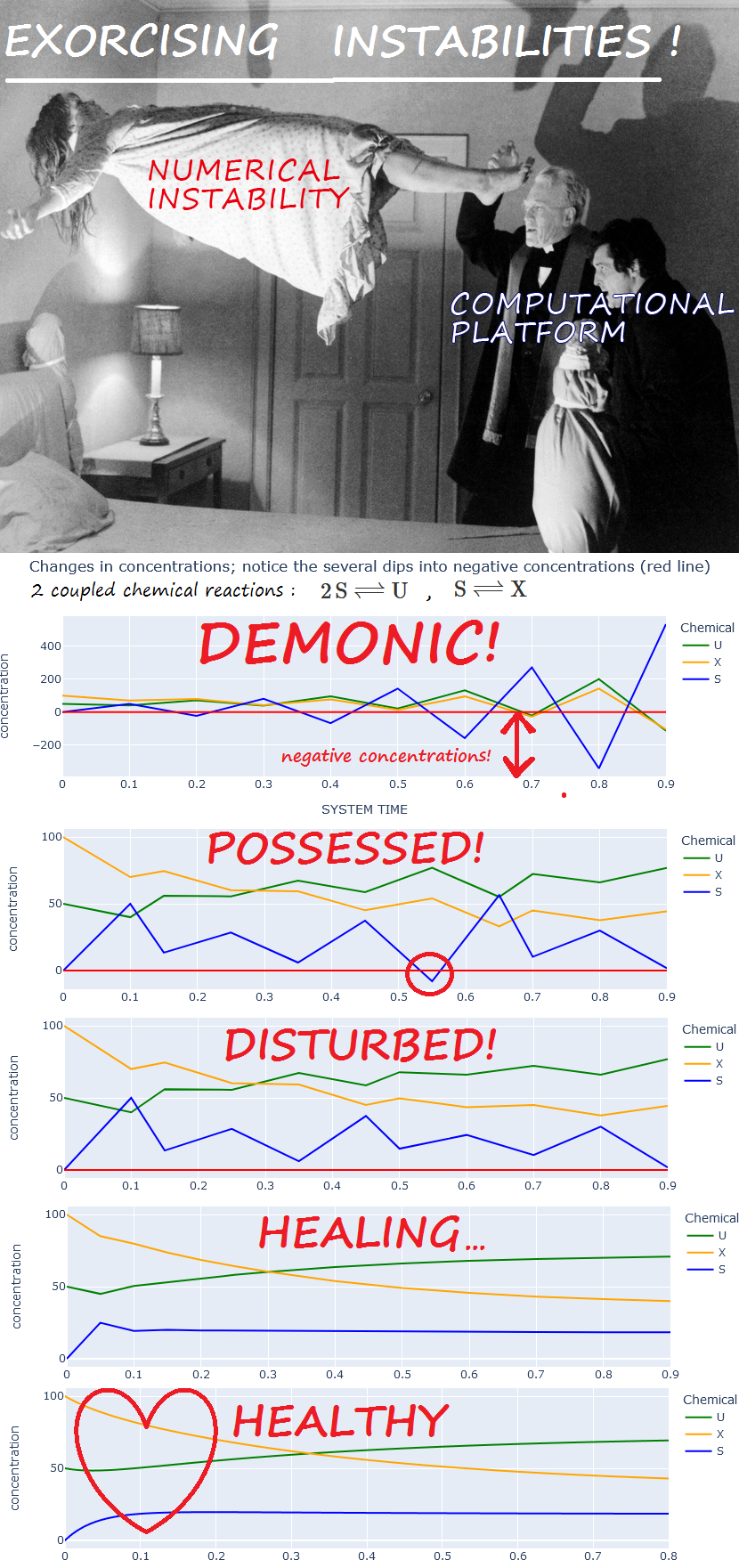
Detection and Automated Correction of Some Instability

At present, Life123 uses negative concentrations, plus multiple heuristics, as a proxy for numerical instability. This appears to catch "the worst offenders", but not all cases, of instability.

Whenever an individual reaction - or group of reactions - causes any chemical concentration to go negative (under any of the 3 scenarios above), a python exception of custom type ExcessiveTimeStep (defined in class ReactionDynamics) is raised.

That exception gets caught in the method ReactionDynamics.reaction_step_orchestrator() - which results in the following:

the (partial) execution of the last step gets discarded
the step size gets reduced by a given amount (which the user may modify)
the run (simulation of reactions) automatically resumes from the previous time

The detection and automatic correction of negative concentration values is showcased in the experiment negative_concentrations_1

Macromolecules

Version Beta 28 introduced initial support for macromolecules.

Occupancy of binding sites on a macromolecule, as a function of Ligand Concentration, can now be modeled. (For example, Transcription Factors binding to DNA.)

Example:

In upcoming versions, the fractional occupancy values will regulate the rates of reactions catalyzed by the macromolecules...

Examples of usage may be found under Experiments (in the "Single-compartment Reactions" section.)